自発運動,集団運動,現象の数理モデル,分岐解析
生物/無生物の自発運動(集団運動も含む)という身近な現象に興味があり、数理的立場から研究を行なっています。自発運動と一言に言っても対象は幅広いですが、これまでは水面における界面活性粒子の運動を主に研究してきました。この「水‐界面活性剤系」は数学、物理学的にも大変興味深いテーマで、実験、数理モデリング、解析を必要とする未解決問題が沢山あります。
ところで、生物の自律運動を数理モデル化することが出来れば、其処にはどのような数理構造が潜んでいるのでしょうか?無生物系と類似した構造が見られるでしょうか?こんなことを考えながら、日夜研究に励んでいます。



関数解析・無限次元解析・スペクトル解析・確率解析に関連する学際的な研究を志向しています。特に、量子(非可換)確率論を基軸として、量子ホワイトノイズ理論の構築と複雑ネットワークのスペクトル解析に力を入れています。
また、応用数学連携フォーラムでは異分野研究者とのおしゃべり文化を育てたいと願っています。
量子(非可換)確率論・無限次元確率解析・量子ホワイトノイズ理論・複雑ネットワーク・スペクトル

離散可積分系, 離散微分幾何学を研究しています。
可積分系には, 微分方程式の可解性の背後に豊かな数学的構造が存在することが知られています。 微分幾何学の立場から見ると、それは曲線や曲面と言った幾何学的対象の可積分条件に対応しています。可積分系の離散化は、現象を記述する微分方程式モデルをシミュレーションする上で重要です。離散化の手段は一つではなく、可積分系の数学的構造の持つ「よい性質」を保つように離散化することが必要となります。 私はこれを、微分幾何学的な見地から離散化する試みに取り組んでいます。

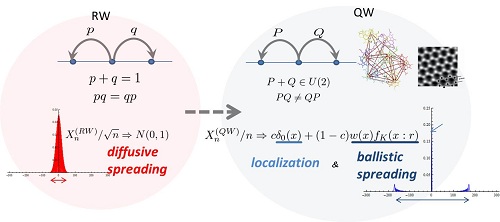
量子ウォークとその応用: 量子ウォークは2000年周辺から、空間構造のある量子探索アルゴリズムの立役者の1つとして脚光を浴びるようになりました。現在ではランダムウォークに対応する微細な世界を記述する素過程の1つになり得ることが期待されており、様々な視点から研究されています。
私の研究では量子ウォークモデルに対する統括的な手法を開発することで、量子ウォークの正体を浮き彫りにすることを目的にしています。そして様々な微細世界の現象の数理モデルとして量子ウォークを適用することで、それらを解明していきます。
http://www.etsuo-segawa.com/jp.html

熱力学、材料科学、生物物理などの数理を研究しています。対象のスケールに応じて適切な数理モデルを考え、数値計算および数学的解析を行っています。
特に、時空間パターンとその安定性を明らかにすることで、熱・粘弾塑性・相分離・化学反応などがどのように相互作用し、どのような機能と結びついているかを調べています。複雑な相互作用系である諸現象を解きほぐし、再構成する中で、融合領域分野の創成を目指します。
固液転移、粘弾塑性、相分離、化学反応、形状記憶、脂質膜、分岐、安定性

諸科学分野で見られる流体現象において、数値解析を援用して安定性解析を行うことで、その現象のメカニズム解明に役立てます。
具体的には、諸科学分野で見られる流体現象の本質的な物理現象を抽出し、主な支配方程式にNavier-Stokes方程式を含む数理モデルを設定した後、数値解析または分岐解析を行います。
流体力学、数値解析、分岐解析


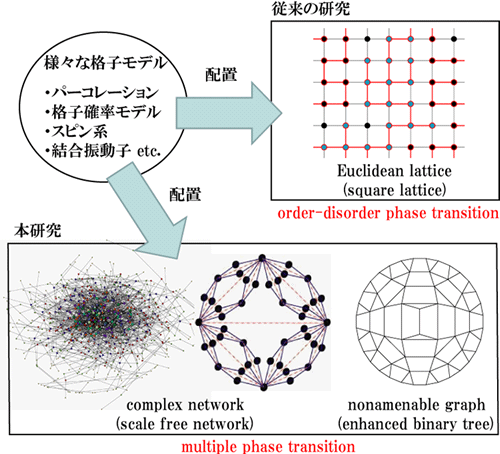
複雑に結合した系の統計物理: complex networkとnonamenable graph上の相転移現象。複雑な結合を持つグラフ“複雑ネットワーク”は近年様々な分野で研究が行われています。ネットワーク上にパーコレーション、格子確率過程、スピンといった格子モデルを配置した場合、従来のユークリッド格子系とは大きく異なる振舞いを示すことが明らかになってきました。
本研究では、複雑ネットワーク、nonamenable graphにおける相転移を調べ、ネットワーク・トポロジーとダイナミクスの関係を明らかにします。
http://www.math.is.tohoku.ac.jp/~hasegawa/index-jpn.html

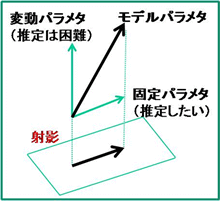
情報幾何学の神経科学等のデータ解析への応用:脳活動などの時間変動するデータに対しては、定常性を仮定した従来のデータ解析手法では、必ずしも十分な情報が得られません。そこで、時間変動するデータから、変動しない情報のみを幾何学的に「射影」して取り出す数学的方法を考案します。
諸分野のデータをこのような視点で捉えることで、これまでには見えなかった情報を検出するという形で、共同研究で貢献したいと考えています。

波面の幾何学、可積分幾何、スペシャル幾何
アピールポイント:12次元の波面が気に入っていて目に見えるようになりました。ここに現れる例外群が関係するスペシャル幾何は、物理の世界と繋がる不思議な幾何です。また、可積分幾何はグラフィックを始めとする応用に繋がる重要な幾何です。
波面,調和写像,可積分系 wave fronts, harmonic maps, integrable systems

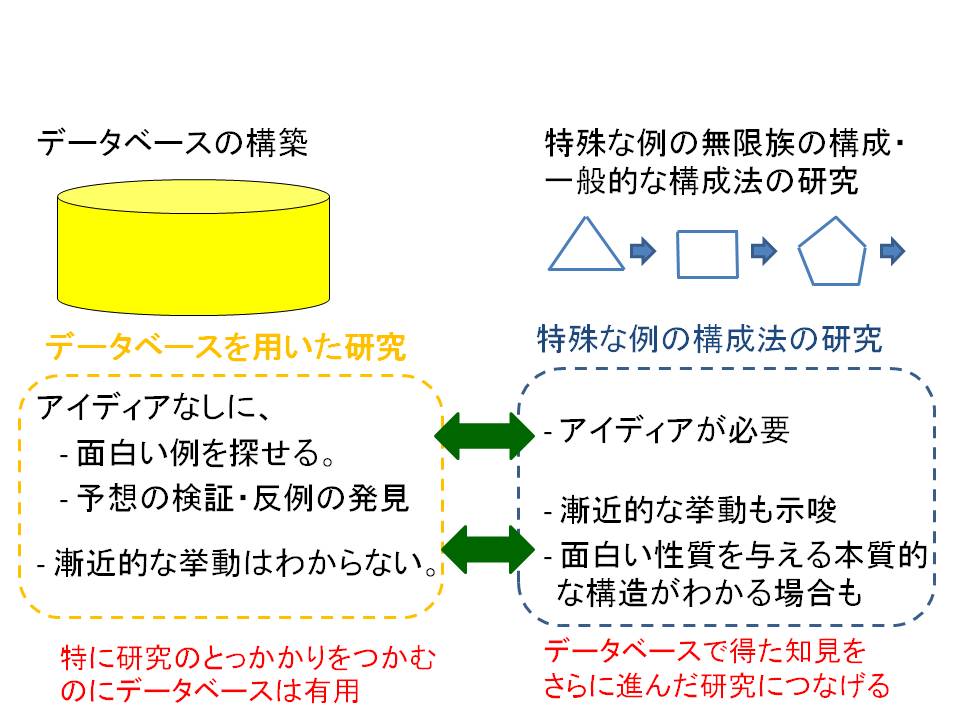
幾何構造のデータベース構築と面白い構造の構成法の研究:計算幾何や最適化で基本的な対象である点配置、超平面配置、多面体、線形計画問題、線形相補性問題などさまざまな対象の組合せ構造の大規模な分類を行い、それらをデータベースとして用いて、未解決問題の妥当性の検証や反例の構成・面白い例の発見を目指した研究をしています。
一方、データベースがカバーする範囲はあくまで有限であることから、面白い例の無限族の構成や一般的な構成法の研究を併せて行い、さらなる理論的考察を行います。上記対象以外にも研究対象を広げていき、さまざまな分野と連携することを目指したいと考えています。

粒子が不連続に動く様子を描写した、飛躍型マルコフ過程について物理学等の分野と連携することを目指しながら、研究を行っています。

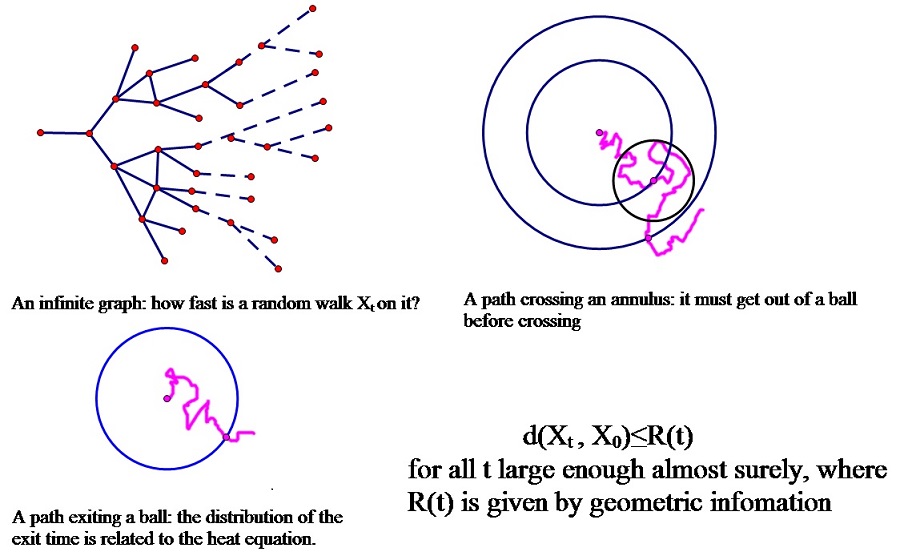
Dirichlet forms and Markov processes on metric measure spaces : I worked on the large time behaviour of jump processes, with a focus on continuous time random walks on weighted graphs. Typical problems include recurrence, conservativeness and escape rates of a Markov process. We aim at giving criteria in terms of geometric information of the underlying space. The fun part is the rich connection between analysis and probability, and it is necessary to combine tools from both areas. For example, estimates of solutions of the heat equation gives information about the exit time of a ball. On the other hand, estimates of the occupation time of a random walk on a modified graph helps analytic arguments to go through on the original graph. I am also interested in many other things related to the heat equation, especially criteria for heat kernel estimates in terms of functional inequalities.