spontaneous motion, collective motion, mathematical modelling, bifurcation analysis
I am interested in spontaneous motion, as well as collective motion, of living and nonliving things. From mathematical point of view, we have been studying the spontaneous motion of surfactant particles at the air-water interface by means of experiment, mathematical modelling and analysis. The surfactant-water systems attract scientists because there are many problems among them, which are relating to mathematics and physics, and sometimes chemistry and biology.
I hope that we find a mathematical structure in biological systems, which is possibly similar to the one in nonliving systems.



I am interested in various topics in functional analysis, infinite dimensional analysis, spectral analysis, and stochastic analysis. In particular, I am currently devoted to quantum white noise theory and spectral analysis of complex networks along the lines of quantum (noncommutative) probability.
I am running the Applied Mathematics Forum (AMF) to encourage communication with researchers with various backgrounds.
Quantum (noncommutative) probability, infinite dimensional stochastic analysis, quantum white noise theory, complex networks, spectrum

I am interested in the discrete integrable systems and discrete differential geometry. In integrable systems, it is known that there are mathematical structures behind the integrability of differential equations. From a geometrical point of view, the integrability corresponds to the integrability of curves and surfaces. On the other hand, the discretization of the integrable systems is important in simulating differential equations. There are several ways to discrete these equations. We are required to discretize integrable systems preserving a mathematical structure. I am studying this from the aspect of differential geometry.

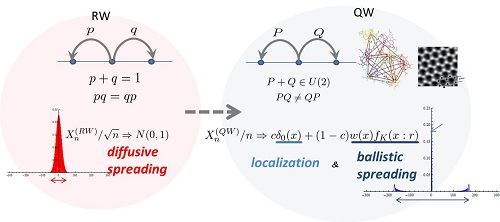
Applications of quantum walks: Quantum walks have attracted many researchers since its efficiency of applications to quantum spatial search algorithm was shown around 2000-2005. Now a day, quantum walk is expected to be an elementary walk describing nanoscopic world as quantum analogue of random walks. In my study, I develop abstractive expressions of quantum walks to obtain an essential figure of quantum walk. Moreover I study applications of quantum walks to various kinds of phenomena in the quantum world.
http://www.etsuo-segawa.com/index.html

My research interests are in thermodynamics, materials science, biophysics. My research consists of mathematical modelling, numerical calculation, and mathematical analysis, depending on the scale of the object of interest. One of the aims is to investigate effects of interactions between factors (e.g., heat, viscoelastoplasticity, phase separation, and chemical reaction) and the resulting functions by clarifying spatio-temporal patterns and their stability. I work towards creating new interdisciplinary scientific fields while unraveling and reconstructing various phenomena of complex interacting systems.
solid-liquid phase transition, viscoelastoplasticity, phase separation, chemical reaction, shape memory, lipid membrane, bifurcation, stability

I am interested in uses of stability analysis to fluid flows in some scientific fields, using numerical calculations.
In particular, extracting essential aspects from fluid flows in some scientific fields, constructing mathematical modelling involving Navier-Stokes equations, I operate bifurcation analysis of the solution of the mathematical model, numerically.
Fluid dynamics, Numerical analysis, Bifurcation analysis

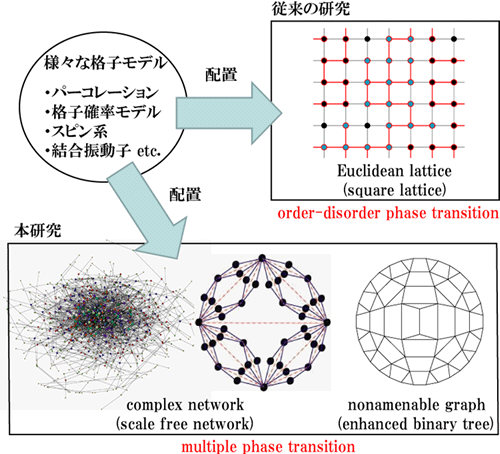
Statistical Physics of Complex Networked Systems: Phase Transitions on Complex Networks and Nonamenable Graphs. Complex networks have been actively studied in recent years. Lattice models (such as percolation, spatial stochastic models, spin models) on complex networks exhibit considerably different behaviors from regular lattice systems. In this project, I will analyze the phase transitions on complex networks and nonamenable graphs, and clarify the relation between network topology and dynamics.
http://www.math.is.tohoku.ac.jp/~hasegawa/

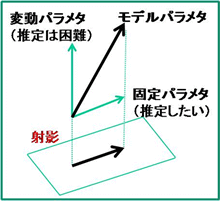
Application of information geometry to data analysis in fields such as neuroscience: Conventional methods for stationary data analysis cannot be applied successfully to non-stationary time series, such as dynamical brain activities. I am developing a mathematical method for extracting invariant information from non-stationary data by using geometric "projections". I hope to collaborate with experts in various areas to illuminate new perspectives and to discover previously-undetectable parameters.

Evolution of hypersurfaces, Integrable geometry, Special Geometry
I love certain 12-dimensional wave front which becomes visible to me. The related exceptional Lie group combines the special geometry with physics. The integrable geometry is important in connection with applications to such as graphics.
wave fronts, harmonic maps, integrable systems

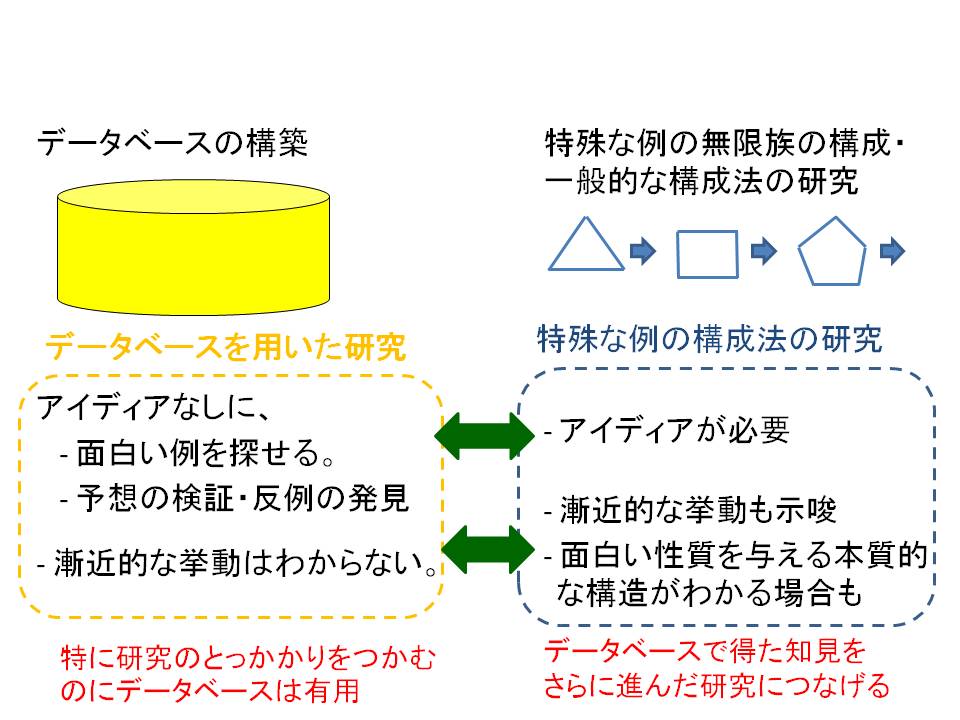
Developing databases of various geometric structures and constructing interesting examples: I am developing databases of various structures such as point configurations, hyperplane arrangements, polytopes, linear programs and linear complementarity problems, which are fundamental objects in computational geometry and optimization. They can be used to check various open conjectures and to find interesting examples. On the other hand, the numbers of instances they can cover are finite and thus I study constrctions of infinite families of interesting examples together with database studies in order to make better use of the databases. Based on the above research, I aim to extend my research area and collaborate with other fields.

Jump Markov processes describe discontinuous movement of particles. The studies on jump Markov processes have developed for the lastd ecade. I am interested in applications of these processes to various fields of science, such as physics, chemistry and so on.

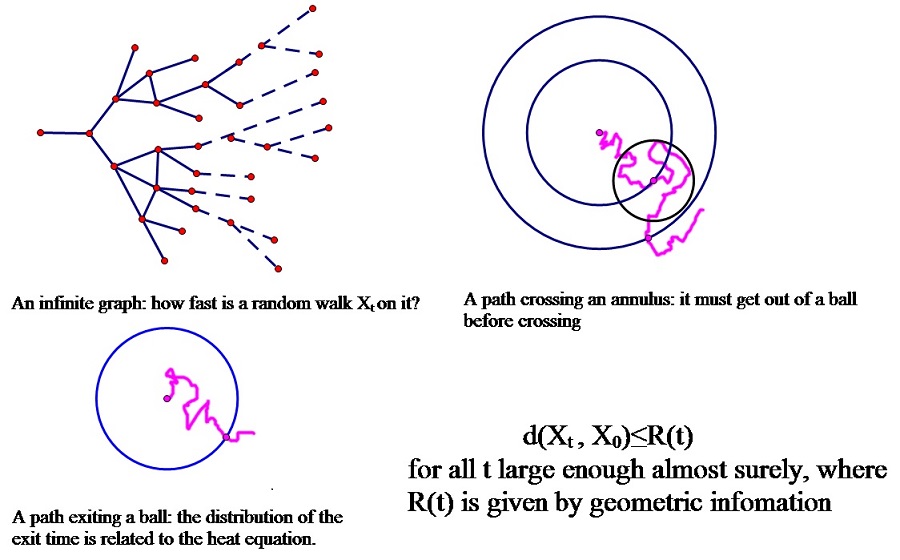
Dirichlet forms and Markov processes on metric measure spaces : I worked on the large time behaviour of jump processes, with a focus on continuous time random walks on weighted graphs. Typical problems include recurrence, conservativeness and escape rates of a Markov process. We aim at giving criteria in terms of geometric information of the underlying space. The fun part is the rich connection between analysis and probability, and it is necessary to combine tools from both areas. For example, estimates of solutions of the heat equation gives information about the exit time of a ball. On the other hand, estimates of the occupation time of a random walk on a modified graph helps analytic arguments to go through on the original graph. I am also interested in many other things related to the heat equation, especially criteria for heat kernel estimates in terms of functional inequalities.